While investigating how string theory can be used to explain certain physical phenomena, scientists at the Indian Institute of Science (IISc) have stumbled upon on a new series representation for the irrational number pi. It provides an easier way to extract pi from calculations involved in deciphering processes like the quantum scattering of high-energy particles.
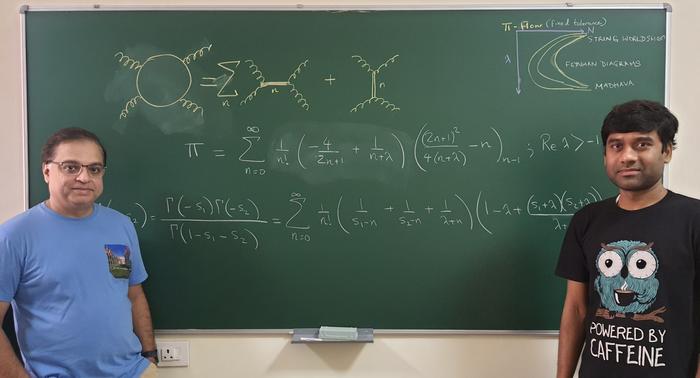
Credit: Manu Y
While investigating how string theory can be used to explain certain physical phenomena, scientists at the Indian Institute of Science (IISc) have stumbled upon on a new series representation for the irrational number pi. It provides an easier way to extract pi from calculations involved in deciphering processes like the quantum scattering of high-energy particles.
The new formula under a certain limit closely reaches the representation of pi suggested by Indian mathematician Sangamagrama Madhava in the 15th century, which was the first ever series for pi recorded in history. The study was carried out by Arnab Saha, a post-doc and Aninda Sinha, Professor at Centre for High Energy Physics (CHEP), and published in Physical Review Letters.
“Our efforts, initially, were never to find a way to look at pi. All we were doing was studying high-energy physics in quantum theory and trying to develop a model with fewer and more accurate parameters to understand how particles interact. We were excited when we got a new way to look at pi,” Sinha says.
Sinha’s group is interested in string theory – the theoretical framework that presumes that all quantum processes in nature simply use different modes of vibrations plucked on a string. Their work focuses on how high energy particles interact with each other – such as protons smashing together in the Large Hadron Collider – and in what ways we can look at them using as few and as simple factors as possible. This way of representing complex interactions belongs to the category of “optimisation problems.” Modelling such processes is not easy because there are several parameters that need to be taken into account for each moving particle – its mass, its vibrations, the degrees of freedom available for its movement, and so on.
Saha, who has been working on the optimisation problem, was looking for ways to efficiently represent these particle interactions. To develop an efficient model, he and Sinha decided to club two mathematical tools: the Euler-Beta Function and the Feynman Diagram. Euler-Beta functions are mathematical functions used to solve problems in diverse areas of physics and engineering, including machine learning. The Feynman Diagram is a mathematical representation that explains the energy exchange that happens while two particles interact and scatter.
What the team found was not only an efficient model that could explain particle interaction, but also a series representation of pi.
In mathematics, a series is used to represent a parameter such as pi in its component form. If pi is the “dish” then the series is the “recipe”. Pi can be represented as a combination of many numbers of parameters (or ingredients). Finding the correct number and combination of these parameters to reach close to the exact value of pi rapidly has been a challenge. The series that Sinha and Saha have stumbled upon combines specific parameters in such a way that scientists can rapidly arrive at the value of pi, which can then be incorporated in calculations, like those involved in deciphering scattering of high-energy particles.
“Physicists (and mathematicians) have missed this so far since they did not have the right tools, which were only found through work we have been doing with collaborators over the last three years or so,” Sinha explains. “In the early 1970s, scientists briefly examined this line of research but quickly abandoned it since it was too complicated.”
Although the findings are theoretical at this stage, it is not impossible that they may lead to practical applications in the future. Sinha points to how Paul Dirac worked on the mathematics of the motion and existence of electrons in 1928, but never thought that his findings would later provide clues to the discovery of the positron, and then to the design of Positron Emission Tomography (PET) used to scan the body for diseases and abnormalities. “Doing this kind of work, although it may not see an immediate application in daily life, gives the pure pleasure of doing theory for the sake of doing it,” Sinha adds.
Journal
Physical Review Letters
Article Title
Field Theory Expansions of String Theory Amplitudes
Article Publication Date
28-May-2024
Discover more from Science
Subscribe to get the latest posts sent to your email.


