Think simpler, flow faster

Analyzing and simulating fluid flow is a challenging mathematical problem that impacts various scenarios, including video game engines, ocean current modeling and hurricane forecasting. The core of this challenge lies in solving the Navier–Stokes equations, a set of classical equations that describe fluid dynamics. Recently, deep learning has emerged as a powerful tool to accelerate equation solving. Using this technique, a team designed a novel approach that can provide accurate solutions 1,000 times faster than traditional equation solvers. The team’s study was published June 26 in Intelligent Computing, a Science Partner Journal.

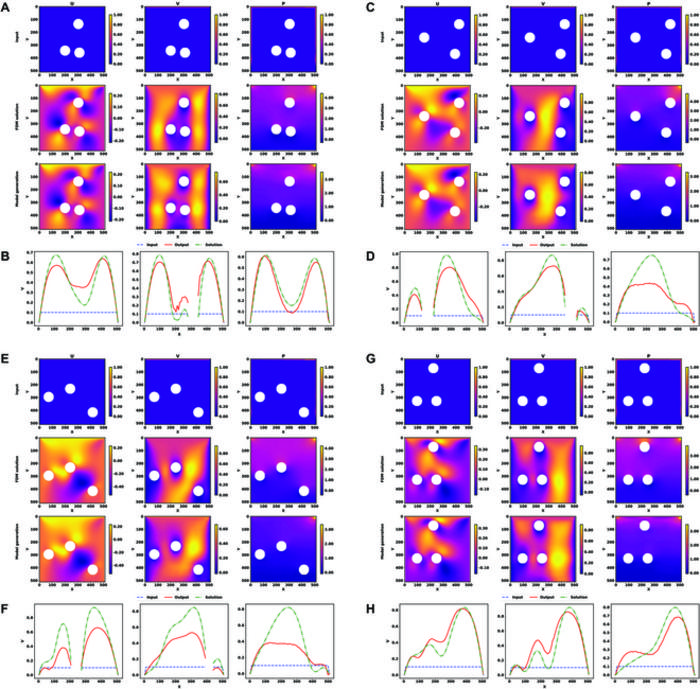
The team tested their approach on a three-variable lid-driven cavity flow problem in a large 512 × 512 computational domain. In the experiment, conducted on a consumer desktop system with an Intel Core i5 8400 processor, their method achieved inference latencies of just 7 milliseconds per input, a great improvement compared to the 10 seconds required by traditional finite difference methods.

Apart from being swift, the new deep learning approach is also low-cost and highly adaptable, thus could be used to make real-time predictions on everyday digital devices. It integrates the efficiency of supervised learning techniques with the necessary physics of traditional methods.

Although other supervised learning models can rapidly simulate and predict the closest numerical solutions to the Navier–Stokes equations, their performance is constrained by the labeled training data, which could lack the size, diversity and fundamental physical information needed to solve the equations.

To work around data-driven limitations and reduce computation load, the team trained a series of models stage by stage in a weakly supervised way. Initially, only a minimal amount of pre-computed “warm-up” data was used to facilitate model initialization. This allowed the base models to quickly adapt to the fundamental dynamics of fluid flow before progressing to more complex scenarios and eliminated the need for extensive labeled datasets.

All models are based on a convolutional U-Net architecture, which the team customized for complex fluid dynamics problems. As a modified autoencoder, the U-Net consists of an encoder that compresses the input data into compact representations, and a decoder that reconstructs this data back into high-resolution outputs. The encoder and decoder are connected through skip connections, which help preserve important features and improve the quality of the outputs.

To ensure the outputs adhere to the necessary constraints, the team also developed a custom loss function that incorporates both data-driven and physics-informed components.

Like traditional methods, the team’s approach uses a 2D matrix to represent the computational domain, which sets the determining constraints of the fluid dynamics problems. The constraints include geometric constraints such as the size and shape of the domain, physical constraints such as the physical features of the flow and applicable physical laws, and boundary conditions that define the problems mathematically. This format allows unknown variables to be directly integrated into the constraints as part of the input data so that the trained models can handle various boundary conditions and geometries, including unseen complicated cases.