Quantum walks represent a frontier in computational theory, harnessing the innate properties of quantum mechanics to outperform classical algorithms. By employing principles such as superposition, interference, and entanglement, researchers are exploring their potential for a variety of practical applications ranging from quantum computing to graph theory. In a recent systematic review published by a team from the National Innovation Institute of Defense Technology at the Academy of Military Sciences in China, the authors offer a comprehensive examination of quantum walks and their implications for the future of computing. This review, released on November 13, 2024, in the journal Intelligent Computing, delves into the theory, implementation strategies, and application areas of quantum walk computing.
In essence, quantum walks serve as the quantum parallel to classical random walks, providing a robust framework for constructing advanced algorithms capable of performing tasks that are cumbersome or intractable for classical computers. The review discusses various types of quantum walks, including discrete-time, continuous-time, discontinuous, and nonunitary quantum walks, each of which showcases distinct characteristics and computational advantages. This categorization lays the groundwork for understanding how different quantum systems interact with classical data structures and problem spaces.
Discrete-time quantum walks operate in a step-wise fashion dictated by probabilistic coin flips, utilizing models that include the Hadamard and Grover walks. These models serve as platforms for graph-based movement, facilitating operations performed on classical data while leveraging quantum phenomena. On the other hand, continuous-time quantum walks function on graphs by employing time-independent Hamiltonians, a feature that makes them particularly effective for spatial searches and traversal challenges within intricate graph networks. The review emphasizes how these models not only boost computational speed but also maintain a probability distribution that mirrors classical random walks under certain conditions.
Discontinuous quantum walks stand out by combining attributes of both discrete and continuous models, thus enhancing their potential for universal computation. This unique construct allows for seamless state transfers and exhibits pathways towards achieving perfect state exchange between quantum systems. Nonunitary quantum walks, which encompass stochastic and open quantum walks, broaden the scope by serving as models for open quantum systems. Their applications extend into domains such as photosynthesis simulation and quantum Markov processes, showcasing their versatility and ability to model complex quantum interactions.
The authors of the review further highlight the dual approaches to physically implementing quantum walks: analog and digital physical simulations. Analog implementations employ solid-state, optical, and photonic systems to directly realize specific Hamiltonians. This method is advantageous for scaling particle numbers and dimensions, yet it bears limitations related to error correction and fault tolerance, presenting significant hurdles for simulating larger graphs effectively.
Conversely, digital physical simulations establish quantum circuits to facilitate quantum walks while allowing for error correction and fault tolerance to some degree. The authors acknowledge that while circuit design presents its own set of challenges, successful digital implementations can lead to significant quantum speedups and offer the capability to simulate a wide array of graph configurations. These differing physical implementations underline the adaptability of quantum walk models, inviting further exploration into how real-world applications can benefit from quantum computational strategies.
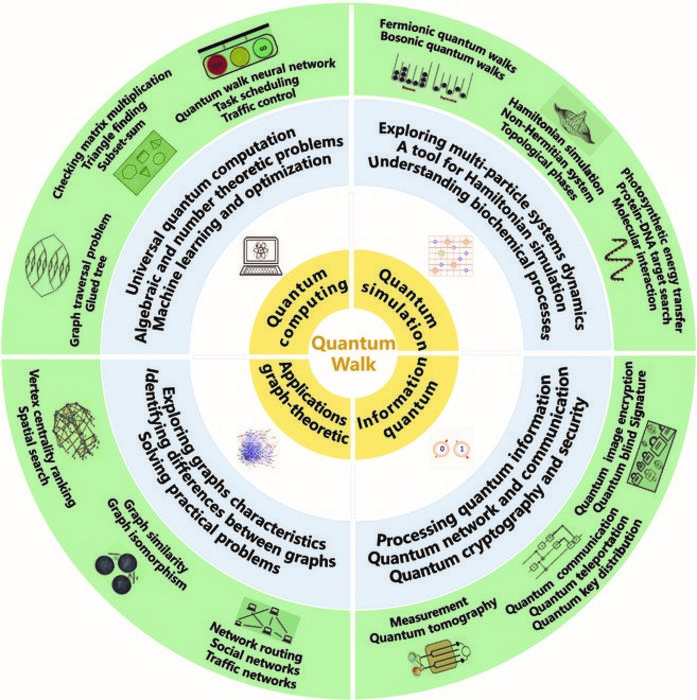
Four primary categories emerge when exploring applications of quantum walks: quantum computing, quantum simulation, quantum information processing, and graph-theoretic applications. In the realm of quantum computing, quantum walks prove to be instrumental in achieving universal quantum computation. They enable speedy resolutions to numerous algebraic and number-theoretic problems and are being integrated into machine learning and optimization strategies. Notably, the capacity for quantum walks to harness computational resources more effectively than classical counterparts showcases their promise in transforming various computing landscapes.
Within quantum simulations, quantum walks function as vital instruments for probing the behaviors of unmanageable quantum systems. They unlock insights into complex quantum phenomena, which traditional analytical techniques may struggle to unravel. This power extends to applications that encompass the simulation of multi-particle systems and the modeling of biochemical processes, providing invaluable tools for researchers aiming to decode intricate interactions present in fundamental physics.
Quantum information processing stands to gain significantly from the empirical capabilities of quantum walks, with applications spanning the preparation, manipulation, characterization, and transmission of quantum states. This also permeates into realms such as quantum cryptography and security, highlighting the potential for quantum walks to secure communications against classical attack strategies, thus ushering in a new era of information technology.
In terms of graph-theoretic applications, quantum walks linked to graph structures represent promising avenues for addressing combinatorial problems and enhancing network functions. Researchers are leveraging quantum walks to assess graph properties, gauge vertex centrality, and discern structural contrasts across diverse graph architectures. This intersection of quantum mechanics and graph theory reveals new paths for analyzing complex systems, potentially leading to breakthroughs in understanding and optimizing networks.
Despite the significant advancements in this field, practical challenges persist in realizing the full potential of quantum walk computing. Among these challenges are the need for effective algorithm development, scaling of physical implementations, and the integration of error correction and fault tolerance frameworks. These hurdles not only serve as areas for improvement but also enrich the research landscape, offering pathways for future explorations and innovations.
The systematic review elucidates the evolving landscape of quantum walks, situating them at the nexus of quantum computing and practical applications. With their unique capabilities to transcend classical limitations, quantum walks might herald a burgeoning era in computational theory and practice, potentially revolutionizing how we approach algorithm design, simulations, and complex problem-solving in diverse domains.
Subject of Research: Quantum Walk Computing
Article Title: Quantum Walk Computing: Theory, Implementation, and Application
News Publication Date: 13-Nov-2024
Web References: DOI 10.34133/icomputing.0097
References: N/A
Image Credits: Xiaogang Qiang, Shixin Ma and Haijing Song
Keywords: Quantum walks, quantum computing, algorithms, simulations, quantum systems, graph theory, entanglement, information processing, quantum cryptography, optimization.