People underestimate the probability of including at least one minority member in a group

Niigata, Japan – Human society includes various minority groups. However, it is often difficult to know whether someone is a minority member simply by looking at the person, as minority traits may not be visually apparent (e.g., sexual orientation, color vision deficiency). In addition, minorities may hide their minority traits or identities. Consequently, we may have been unaware of the presence of minorities in daily life. Probabilistic thinking is critical in such uncertain situations. The people with whom we interact in our daily lives are typically a group of several dozen individuals (e.g., a school class). How do we judge the probability of including at least one minority member in such groups? For example, how does a school teacher estimate the probability of having a minority in the class? Cognitive psychology states that humans often make unrealistic judgments about probabilities, such as risk. So, do we also misperceive the probability of minority inclusion in a group or can we accurately assess the probability through heuristics or knowledge?

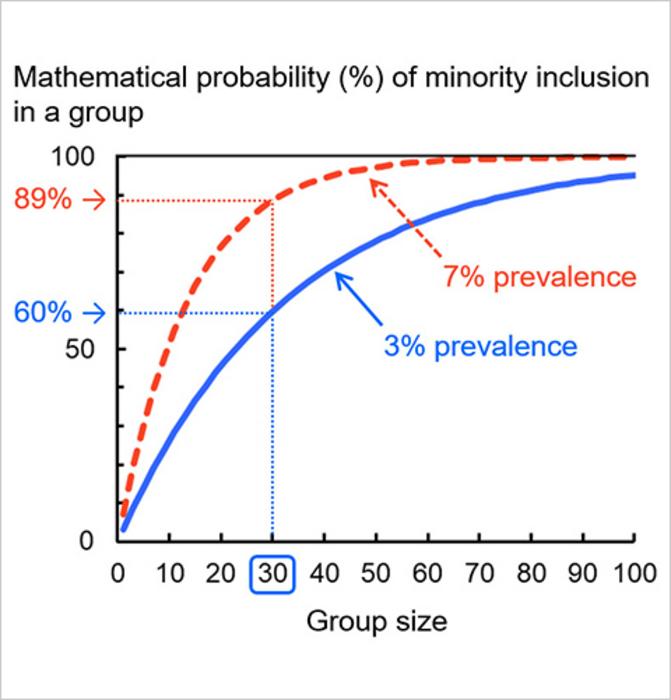
Associate Professor Niimi of Niigata University demonstrated that people unrealistically underestimate such probabilities. First, we examine how the probabilities are computed mathematically. If the prevalence of the minority in question is 0.03 (3%) and the group size is 30, the probability of including one or more minority members in the group is one minus the probability that all 30 members are NOT the minority. Because the probability that one person is not a minority is 0.97, the probability of minority inclusion is given by 1 – (0.97)³⁰ (if there is no other information). The computer tells us that the result is 0.60 (60%). When the minority prevalence is 7%, it increases to 89%. These mathematical probabilities appear to be higher than those of naïve intuition.

Indeed, most respondents estimated probabilities far below the mathematical probabilities. The second image shows examples of the questions and results. Approximately 90% of the respondents estimated below-mathematical probabilities, and the majority of the estimates were lower than 10%. This underestimation was repeatedly observed under a variety of conditions (online worker and student samples, revised wording, etc.).

Why are the probabilities of minority inclusion underestimated? Is this a result of prejudice or stereotyping against minorities? The answer was “No.” The same underestimation occurred even when minorities unlikely to be associated with negative stereotypes were used (e.g., people with absolute pitch and fictional minorities). Of course, the mathematical calculations cannot be performed mentally. No wonder the respondents’ estimates were inaccurate. The problem was why the estimates were not random, but strongly biased toward underestimation. Even if one does not know how to calculate it, one may have learned from daily experience that the probability of inclusion is much higher than the prevalence (e.g., the probability of including a woman in a group of randomly selected 100 individuals should be greater than 50%). However, the present results suggest that most people are unfamiliar with the concept of probability of inclusion and do not know how to think about it. Further analysis revealed that the major source of underestimation was the use of heuristics, such as ignoring group size and reporting prevalence, or calculating the expected value of the number of minorities. Although most heuristics were erroneous, some yielded relatively reasonable estimates (e.g., assuming a high probability if the expected value exceeded one).

Underestimating the probability of minority inclusion may lead to the misconception that minorities are irrelevant in our daily lives. However, there was one promising finding in the present study. When the respondents were given the mathematical probability of minority inclusion, their attitudes changed in favor of inclusive views about minorities compared to conditions in which mathematical probability was not given. Knowledge may compensate for cognitive bias.