The topological photonics plays an important role in the fields of fundamental physics and photonic devices. The Kagome model, the Su-Schrieffer-Heeger (SSH) model and the other topological models are used as a platform to study the novel physics phenomenon, and guide to design novel photonic devices such as topologically protected laser and robust transmission device. Till now, researchers usually judge the topological states in a photonic crystal based on three criterions. The topological invariant, including Chern Number, winding number and Z2 topological invariant; the eigenvalue distributions or gaps in the band of photonics crystal; the electric field distributions of the topological states. Almost all the previous methods rely on the band structures in the momentum spaces. However, it is generally complicated to analyze the topological properties in momentum space, especially if there are perturbations in the system. The perturbations will even cause the bandgap closing of topological system, which will bring difficulty to analyze the topological in momentum space.

Credit: Rui Ma , Qiuchen Yan , Yihao Luo , Yandong Li , Xingyuan Wang , Cuicui Lu , Xiaoyong Hu , Qihuang Gong
The topological photonics plays an important role in the fields of fundamental physics and photonic devices. The Kagome model, the Su-Schrieffer-Heeger (SSH) model and the other topological models are used as a platform to study the novel physics phenomenon, and guide to design novel photonic devices such as topologically protected laser and robust transmission device. Till now, researchers usually judge the topological states in a photonic crystal based on three criterions. The topological invariant, including Chern Number, winding number and Z2 topological invariant; the eigenvalue distributions or gaps in the band of photonics crystal; the electric field distributions of the topological states. Almost all the previous methods rely on the band structures in the momentum spaces. However, it is generally complicated to analyze the topological properties in momentum space, especially if there are perturbations in the system. The perturbations will even cause the bandgap closing of topological system, which will bring difficulty to analyze the topological in momentum space.
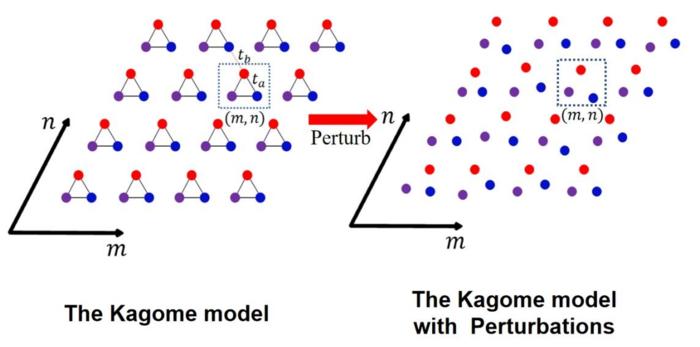
Researchers led by Prof. Xiaoyong Hu at Peking University, China, are interested in the topological photonics. They propose an interdisciplinary approach to study the topological systems through the information entropy (IE) in real space. The Kagome model is used as an example of theoretical calculation, and the disappearing process of its topological edge states (TESs) is observed with IE. The IE method can be used to analyze the TESs mode distributions and topological phase transition. This method can also be extended to SSH model and the valley-Hall photonic crystal. They provide a method to study topological photonic phase based on information theory, and brings inspiration to analyze the physical properties by taking advantage of interdisciplinarity. The work entitled “Information-entropy enabled identifying topological photonic phase in real space” was published on Frontiers of Optoelectronics (published on Apr. 29, 2024).
Journal
Frontiers of Optoelectronics
Method of Research
Experimental study
Subject of Research
Not applicable
Article Title
Information-entropy enabled identifying topological photonic phase in real space
Article Publication Date
29-Apr-2024