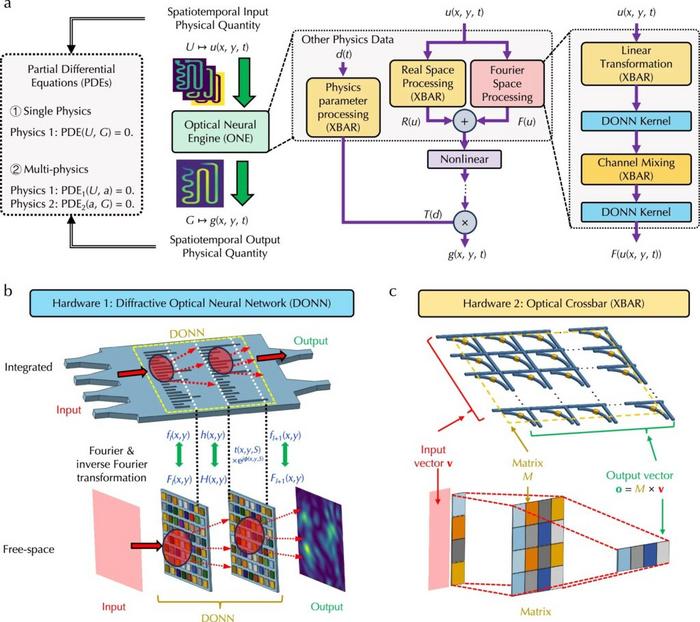
In a groundbreaking advancement bridging the worlds of photonics and computational mathematics, researchers at the University of Utah have unveiled an innovative optical system that revolutionizes the way partial differential equations (PDEs) are solved. These equations, fundamental in describing the behavior of physical phenomena ranging from fluid dynamics to electromagnetism, have long posed significant computational challenges due to their complexity and the intensive resources required for digital simulations. The team’s newly developed “optical neural engine” (ONE) harnesses the unique properties of light to represent and process these equations, delivering solutions with unprecedented speed and energy efficiency.
Partial differential equations function as mathematical expressions interlacing multiple variables, capturing how physical quantities evolve over space and time. Traditionally, scientists and engineers rely on immense numerical simulations that require powerful electronic processors and substantial energy consumption to approximate PDE solutions. Existing computational methods—whether through direct numerical approaches or electronic neural networks—struggle to balance precision, speed, and scalability, especially when tackling large-scale scientific problems with intricate boundary conditions.
The University of Utah team, led by Assistant Professor Weilu Gao and Ph.D. candidate Ruiyang Chen, has confronted this challenge by reimagining PDE computation through an optical framework. Their ONE device fundamentally departs from digital paradigms by encoding PDE variables as distinct attributes of light waves, including intensity, phase, and polarization. The light, modulated to represent an initial state, traverses a sequence of custom-designed diffractive optical elements and matrix multipliers, dynamically altering its properties to embody the PDE solution as it emerges.
At the core of this approach lies a sophisticated interplay between photonics and neural network principles. Neural networks traditionally process inputs by propagating signals through layered computational nodes, each applying weighted transformations to steer the network towards a final output. The optical neural engine replicates this process in the physical domain, where photons carry information across diffractive surfaces that perform matrix multiplications and function approximations akin to digital neurons. This physical embodiment sidesteps the bottlenecks of electronic signal processing, leveraging the inherent parallelism and speed of light propagation.
One of the key advantages of the ONE system is its remarkable acceleration of the machine learning workflow central to solving PDEs. Electronic neural networks, while powerful, consume considerable energy and take longer to converge on solutions. The optical method requires significantly less power, as photons naturally propagate without resistive losses inherent in electronic circuits, and computation occurs at the speed of light within the optical hardware. According to the research team, this translates to dramatic reductions in both execution time and operational costs for complex PDE problems.
The practical applications demonstrated by the ONE device underscore its versatility. The researchers tested the system on diverse PDEs including the Darcy flow equation, which models fluid movement through porous media; the magnetostatic Poisson’s equation relevant to demagnetization studies; and the Navier-Stokes equation governing incompressible fluids. In each case, the optical neural engine successfully learned mappings between input parameters and output physical quantities, predicting solutions without resorting to traditional experimental or computational heavy lifting.
As Professor Gao explains, “The Darcy flow equation, for instance, depicts how fluids navigate through materials filled with tiny pores. Our optical neural engine effectively internalizes the relationship between permeability and pressure within that medium, allowing it to anticipate fluid behavior purely from encoded light signals.” This capability promises transformative impacts in fields such as geology, environmental engineering, and even microchip design, where modeling complex interactions swiftly and accurately is paramount.
Beyond performance, the ONE’s optical paradigm introduces new opportunities for real-time scientific computations that were previously impractical. Situations demanding near-instantaneous PDE solutions—such as adaptive control systems, weather prediction, or biomedical imaging—could greatly benefit from integration with optical neural components. The research opens a pathway toward photonic computing platforms capable of handling dynamic, high-dimensional data with efficiency unattainable by existing electronic processors.
The study, published in Nature Communications, not only presents the hardware innovation but also details the computational modeling substantiating the ONE’s functionality. Through extensive simulation and experimental verification, the team demonstrated that the optical components perform matrix multiplications and nonlinear transformations integral to neural network operation with high fidelity. This foundational work paves the way for scaling the optical neural engine to tackle more complex PDE systems and potentially coupling it with electronic components for hybrid computational architectures.
Supporting the advancement are co-authors from both the University of Utah and Lawrence Berkeley National Laboratory, including Zhi Yao, Andrew Nonaka, Minhan Lou, and Jichao Fan, alongside collaborators from the University of Maryland. Their interdisciplinary effort embodies a fusion of electrical engineering, applied physics, and computational mathematics, highlighting the multi-faceted nature of contemporary scientific innovation.
Funding for this research was generously provided by the National Science Foundation, the U.S. Department of Energy, and institutional start-up grants, underscoring the strategic importance of advancing computational methodologies. As the global demand for computational power surges amid challenges in energy consumption and carbon footprint, technologies like the optical neural engine represent a hopeful stride toward greener and faster scientific computing.
In the broader context of machine learning and artificial intelligence, this optical neural engine signifies a provocative shift. While electronic AI chips have evolved rapidly, their reliance on semiconductor transistors imposes limits on processing density and energy efficiency. Photonic-based computation, exemplified by the ONE, offers an alternative frontier where light’s wave properties can perform analog computations inherently suited for complex mathematical operations, potentially leading to a new class of ultrafast, low-power AI hardware.
Ultimately, the University of Utah’s optical neural engine presents a compelling case for integrating optics and machine learning to solve some of science’s intractable problems. By transforming PDEs from abstract equations into dynamically evolving optical signals, the researchers have charted a course toward accelerated discovery and innovation across physics, engineering, and beyond. As this technology matures, it promises to redefine our computational toolkit, enabling scientists to simulate, predict, and understand the complexities of the natural world with a speed and scale never before possible.
Subject of Research: Partial differential equations (PDEs) solved through optical neural networks
Article Title: Optical neural engine for solving scientific partial differential equations
News Publication Date: 17-May-2025
Web References:
https://www.nature.com/articles/s41467-025-59847-3
References:
Gao, W., Chen, R., Yao, Z., Nonaka, A., Lou, M., Fan, J., Yu, C. (2025). Optical neural engine for solving scientific partial differential equations. Nature Communications.
Image Credits: Gao lab, University of Utah
Keywords: Partial differential equations, computational physics, optical neural networks, photonic computing, machine learning, diffractive optics, fluid dynamics, neural engineering